Algoritmus

Martin Korbel

Úvod

  • Co je algoritmus?

    • Postup kroků k vyřešení určitého problému.

    • Přesně definovaný, konečný a proveditelný.

  • Algoritmus používáme každý den:

    • Recept na vaření

    • Návod k montáži nábytku

    • Dopravní trasa na mapě

Co je algoritmizace?

  • Algoritmizace = přeměna řešení problému na sadu kroků (algoritmus).

  • Krokový proces:

    • 1. Porozumění problému

    • 2. Návrh řešení (slovně, vývojové schéma, pseudokód)

    • 3. Implementace v programovacím jazyce (např v Pythonu)

    • 4. Testování a analýza složitosti

Historie

  • Slovo algoritmus pochází ze jména al-Chvárizmí (perský matematik, 9. století).

  • Algoritmy lidé používali dávno před vynálezem počítačů.

  • Vývoj algoritmů je spojen s matematikou, logikou a později s výpočetní technikou.

Starověk a středověk

  • 300 př. n. l. – Eukleidův algoritmus pro výpočet největšího společného dělitele.

  • Indie a Arábie – algoritmy pro výpočty s čísly, základy aritmetiky.

  • 9. století – Muhammad ibn Músá al-Chvárizmí píše díla o aritmetice a algebře.

    • Jeho jméno dalo vznik slovu "algoritmus".

    • Díky němu se do Evropy dostaly arabské číslice.

17.–18. století

  • Blaise Pascal (1623–1662) – sestrojil mechanickou kalkulačku.

  • Gottfried Wilhelm Leibniz (1646–1716) – představil binární soustavu a stroj na násobení.

  • Algoritmy se využívají v astronomii, geometrii a při stavbě tabulek.

19. století

  • Charles Babbage (1791–1871) – navrhl analytický stroj.

  • Ada Lovelace (1815–1852) – první „programátorka“, popsala algoritmus pro výpočet Bernoulliho čísel.

  • Rozvoj matematické logiky – George Boole (1815–1864) – základy booleovské algebry.

20. století – začátek

  • David Hilbert (1900) – kladl otázky řešitelnosti matematických problémů.

  • Alan Turing (1912–1954) – definoval Turingův stroj → teoretický základ algoritmů.

  • John von Neumann – koncepce architektury počítače (program uložený v paměti).

20. století – praxe

  • 1940–1950: vznik prvních elektronických počítačů (ENIAC, UNIVAC).

  • Rozvoj programovacích jazyků: Fortran, COBOL, Lisp.

  • Algoritmy pro řazení, vyhledávání a šifrování.

  • 1970–1980: teorie složitosti (NP-úplnost, algoritmy pro grafy).

  • Algoritmy pronikají do průmyslu a vědy.

21. století

  • Algoritmy jsou všude:

    • internetové vyhledávače

    • sociální sítě

    • kryptografie a bezpečnost

    • umělá inteligence a strojové učení

  • Výzkum složitosti, kvantových algoritmů a optimalizace.

Vlastnosti algoritmu

  • Konečnost – musí skončit po konečném počtu kroků.

  • Determinovanost – každý krok je jednoznačný.

  • Obecnost – algoritmus lze použít na celou třídu úloh.

  • Hromadnost – funguje na více vstupech, nejen na jednom.

Zápis algoritmu

  • Slovní popis

  • Blokové schéma (vývojový diagram)

  • Pseudokód

  • Programovací jazyk

Jednoduchý algoritmus: Najdi maximum ze dvou čísel

  1. Načti číslo A a B.

  2. Porovnej A a B.

  3. Pokud A > B, vypiš A.

  4. Jinak vypiš B.

  5. Konec.

Algoritmus výpočtu faktoriálu

  1. Načti N.

  2. Nastav výsledek = 1.

  3. Opakuj pro i = 1 až N: výsledek = výsledek * i.

  4. Vypiš výsledek.

  5. Konec.

Základní struktury algoritmů

  • Sekvence – kroky jdou za sebou.

  • Větvení (podmínka) – rozhodnutí podle situace.

  • Cykly (opakování) – opakovaný postup.

Jak přistupovat k úloze (metodika)

  1. Přečti a pochop požadavek.

  2. Vymysli příklad ručně (malá data).

  3. Navrhni krokový postup (slovně nebo pseudokódem).

  4. Zapiš kód v Pythonu.

  5. Otestuj na okrajových případech.

  6. Analyzuj složitost (čas / paměť).

  7. Optimalizuj (pokud je potřeba).

Testování a debugování

  • Používej malé příklady (manuálně ověřitelné).

  • Tiskni mezivýsledky (print) během učení.

  • Piš jednoduché unit testy (modul unittest nebo jednoduché asserty).

Pseudokód

Příklad pro cyklus:

---
i = 1
dokud i ≤ 10:
  vypiš i
  i = i + 1
---

Vývojový diagram

  • Obdélník – krok / akce

  • Kosočtverec – podmínka

  • Ovál – začátek/konec

Vývojový diagram

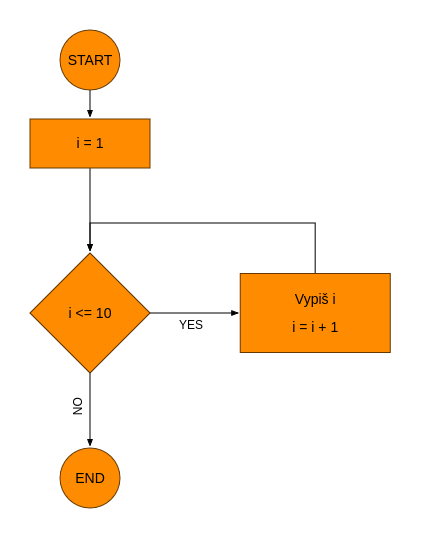
algoritmus

Vývojový diagram

Vyvojovy diagram zarovka

Algoritmická složitost

  • Časová složitost – kolik kroků algoritmus potřebuje.

  • Paměťová složitost – kolik paměti spotřebuje.

  • Označujeme tzv. O-velkou notací:

    • O(1) – konstantní čas

    • O(n) – lineární

    • O(n^2) – kvadratická

    • O(log n) – logaritmická

Shrnutí

  • Algoritmus je přesně definovaný postup řešení problému.

  • Může být zapsán různými způsoby – slovně, diagramem, pseudokódem nebo programem.

  • Každý algoritmus musí mít vlastnosti: konečnost, determinovanost, obecnost.

  • Důležitá je efektivita – časová a paměťová složitost.

  • Algoritmické myšlení je klíčové nejen v informatice, ale i v běžném životě.

Cvičení

Závěrečné otázky pro studenty

  • Co musí splňovat algoritmus?

  • Jaké znáte základní řídicí struktury?

  • Jaký je rozdíl mezi O(n) a O(n^2)?

  • Dokážete uvést příklad algoritmu z běžného života?

Praktická cvičení

  • Sestav algoritmus na výpočet aritmetického průměru čísel.

  • Sestav Eukleidův algoritmus pro výpočet největšího společného dělitele.

  • Sestav algoritmus, který vrátí druhé největší číslo zadané uživatelem.

  • Sestav algoritmus na kontrolu palindromu.

Praktická cvičení

  • Sestav agoritmus pro sečtení všech lichých čísel, až do čísla zadaného uživatelem.

  • Sestav algoritmus, který z půjčené částky, úroku a doby zápůjčky vrátí celkovou částku úvěru.

  • Sestav algoritmus, který pro danou částku vypíše počet bankovek, které má vydat.